what is vortex in 3d cube drawing

Guess what? Cubes are awesome!

No, seriously. If you know how to draw a cube, you will also exist able to sketch whatever three-dimensional grade. Of course, at that place are nuances in every object you lot cull. Still,  the cadre principles, the nuts and bolts of draughtsmanship, stay the same.

They all are in this box.

Allow'due south become them out.

So, this is not one of those '1-2-3 tutorials'. There are thousands of them on the Internet. My goal is to provide you with a skillset enabling you to describe anything. This arroyo will be helpful if you want to deal with concept art, industrial pattern, fantasy/cartoon fine art. They all require sketching from your imagination. It means that you lot demand to be able to draw any object from any angle. You lot will get this knowledge from the lessons. And strengthen it with homework aasigments, provided afterwards each lesson

Now yous will larn the basics of linear perspective through an example of a cube. In later articles, we volition get to much more complicated subjects. If you desire to proceeds equally much benefit from this article as possible, please, kill all destructing factors. Accept a piece of paper and a pen, experiment with the concepts you lot are learning. Believe me, mere reading won't assist much.

What Is Perspective?

Perspective is a system of representation of three-dimensional globe on a flat surface.

Not very complicated, right?

So, here is the most logical and useful concept to go on in mind about perspective.

The cube is seen through the piece of flat glass. The camera is pointed directly at this glass.

The glass is calledPicture Aeroplane (PP). The line fatigued from the camera through PP is chosen Line Of Sight (LOS). I want to stress that LOS is always perpendicular to PP.

"Then, why the hell are y'all telling me all that?" – you may ask.

And hither is why.

We need to know how our lines are positioned in space, relative to something. Camera position is our guiding star. The main idea is that drawing in perspective is a representation of an image from a particular viewing position. There is no paradigm without a viewer.

Drawing a Square

What is a cube? Basically, it consists of 6 square planes fitted together. To draw a cube, nosotros need to know how to position a square in any and all cases, from whatsoever possible viewpoint.

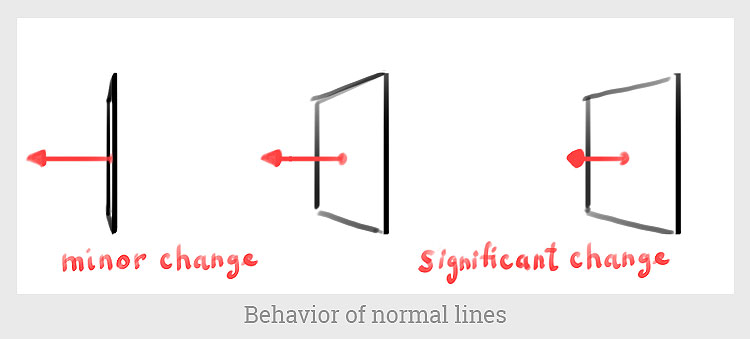
Now nosotros need to add a new nerdy word to our vocabulary –Normal Line or merelyNormal.

If you put the lesser of a pencil on the surface, it volition match the direction of a normal line. Normal is a line perpendicular to the surface.

Simple as that.

Every aeroplane has an space number of these normal lines. For the sake of simplicity, we will draw simply one.

Normals help us determine how we see the surface.

Nosotros have a rectangle and put information technology in front of the camera. If the normal is pointingdirect at the picture plane (90 degrees), then we run across the surface without any distortion. Rectangle – as it is.

And here is the crucial part.

If we tilt our rectangle in whatever direction, the normal line will be no longer perpendicular to PP. The surface of the rectangle shrinks.

How do nosotros determine the direction of a pinch? The normal line tells u.s.a..

The principle is calledCompress Along Normal.

Every aeroplane is compressed only along its normal line.

We can see that plane has changed in proportions. It is narrower because it shrinks along the normal line.

This is e'er the case.

There is no other way to shrink a plane. Only along it's normal. The more than the aeroplane is tilted abroad from the camera, the more than information technology is compressed along its normal line. I will repeat this concept again and again because it's very important. Ane tends to forget these unproblematic things when it comes to drawing.

Converging of Parallel Lines

Another phenomenon. In the instance above, y'all might have noticed that left and correct margins of a rectangle are narrowing towards the top (from the photographic camera view). It happens because they are parallel lines, which recede in space (relative to the picture plane). The lines which are parallel to PP, don't converge.

Sounds difficult? Well, it admittedly should be like that. Learning new things can't be easy.

I think my first steps in cartoon – it felt similar a freakin' hell. It volition get easier over time, I promise yous.

In the articles nearly the perspective, nosotros volition dive deep into the discipline. This volition aid yous to improve your draughtsmanship abilities in the shortest time. Not all readers have a burning desire to improve their drawing skills.

But if you practise, then let's go farther.

Where do the parallel lines converge? I'm certain that you know – on a horizon line. It is written in every fine art book. Generation after generation. This concept is so popular and dogmatic that authors never reconsider its explanation.

But we will.

What Horizon Line Actually Is?

We assume that the bottom of our camera is parallel to the ground plane.

We accept a few horizontal planes in our scene. As these planes lift up, they gradually shrink.

Normal line of a horizontal aeroplane is vertical. That is why everyhorizontalsurface shrinks along thevertical line.

When the airplane shrinks completely, it turns into a single line. Due to a vertical compression this line is horizontal.

This is our Horizon Line.

If your plane cuts the camera right in the centre when you extend it, it means that the aeroplane is shrunk to zero. Information technology is the horizon.

Parallel lines situated on the horizontal planes (no thing which ane) converge on the horizon line. Points of converging are chosen Vanishing Points (VP).

You lot tin can see that every set up of parallel lines hasits own VPs. Typical perspective construction can take Cardinal (CVP), Left (LVP) and Right (RVP).

Ellipses

I didn't tell you that a airplane must have a rectangular shape only.

Why I didn't?

Because a plane tin can exist of any shape.

You but think of it every bit a flat piece of paper. Any shape tin can be cut from information technology. So, we can brand a plane in the course of a circle. So nosotros put it in space and get…

Yes!An ellipse.

Here I pretend, that you've read my article almost basic line piece of work. If not, yous may want to do it now. Because it has some, well, nuts that nosotros volition need.

A plane in the shape of a circle also has its normal line, and this normal is also perpendicular to the plane'south surface.

Hither is a trick near ellipses.

The normal line of ellipse's plane always goes in the same direction as its minor axis.

The principle is but the same as in the example with rectangles.

Only.

The circle has an equal diameter all the way. As the result of a compression (even the slightest one), the diameter volition exist represented by two most important lines: the longest and the shortest ones.

The biggest diameter is a major axis. This line doesn't alter its length, no thing how strong yous tilt the surface.

The smallest diameter is aminor axis. Information technology is perpendicular to the major centrality. It has the same direction as the normal line. It changes the nigh when the circle is tilted abroad from the photographic camera view.

The level of ellipse compression is called thedegree of an ellipse.

If normal of an ellipse's surface is pointing at 90 degrees to the motion picture airplane. And so camera sees a completely open circle.

If the normal is pointing at 45 degrees at PP, the ellipse is called "45-caste ellipse".

The fewer degrees, the more than compression is there.

Ellipses Are Your Rescue Rangers

Nosotros will use ellipses even in cases when there are no visible circular planes in our drawing.

Why?

There are some great advantages.

• Ellipse helps you determine the direction of the surface'southward normal line.

Thus, you know in which direction to shrink your plane when it'south tilted abroad from the viewer.

• Ellipse helps you determine the aeroplane'due south tilt relative to the viewer.

Stronger tilt = stronger compress.

I didn't tell you lot this till the last moment hoping that you have noticed information technology. I believe that the deepest knowledge is gained from your ain feel. Y'all take to fight for it. You lot accept to be courageous and curious. There is no other mode.

So, what I hoped that you guess?

• Ellipse helps yous to find the proportion of a perfect square.

A circumvolve within the square touches each of 4 borders at the midpoints. A circumvolve in perspective (ellipse) does absolutely the same.

Y'all encounter, every ellipse touches foursquare'due south borders at midpoints.

This ise'er the case.

The cube consists of perfect squares. Knowledge of how to construct a foursquare is very of import for our cease goal – cube cartoon.

This commodity may seem a flake too long compared to the end result.

"A cube drawing? Seriously? But information technology should be and so simple… Why practise I need to waste my time reading all this bullshit?".

Proceed your pilus on.

I hope you that the stuff we are learning will before long assist you lot to depict such cool things as tanks, dragons, robots, etc. Of grade, if this is really interesting to you lot.

90 Degree Angle

Apart from square's proportion, we must brand sure that the foursquare has 4 right angles (ninety degrees). We need a proper construction of at least ane angle. Three other will fall into identify.

And over again ellipse is your rescue ranger here.

Information technology will assist you to construct a proper xc° angle between two lines on a unmarried plane. Permit'south draw the correct angle on the basis aeroplane.

Determine proportions of a foursquare from the given viewpoint using your ellipse.

Put a normal line (in this case it's vertical considering the plane is horizontal) in position, depending on how the angle should be turned.

If y'all desire the angle to point straight at the viewer, the normal must be fatigued correct through the middle of the ellipse. Then draw two lines tangent to ellipse from the signal on a vertical line. It will result in an equal shrink of the left and right sides (both 45°) of our box.

If you want to turn the bending clockwise, then you move the normal to the left.

To plough it contraclockwise, employ the same principle.

How much of this normal line should extend beyond the ellipse?

It depends on the degree of an ellipse. The more information technology opens – the longer is the line. You will become information technology better with do. Just exist enlightened of touching the square at the midpoints.

In that location are several ways to consummate the structure of a foursquare in whatever possible position. It depends on the level of desirable perspective extremeness.

The closer the horizon line is to the ellipse (in relation to its size) – themore extreme is the perspective. The lines converge quickly which means that the object is shut to the viewer or it is big. The paradigm looks every bit it is shot with wide angle lens.

If the horizon line isfar away from the ellipse, perspective will be flattened. Lines converge slightly. The object looks minor or is far away from the viewer.

Information technology's a long lens effect.

Here you see that a vertical line sticks outside the ellipse on the same distance in both cases. The lesser angle is the same. The difference ismerely in the perspective extremeness. And once again. The horizon line is perpendicular to the ellipse's normal (pocket-sized axis).

Horizon is an substantially flat airplane which is parallel to that ellipse. This plane is just tilted completely away from the viewer's observation.

Drawing a Cube (Finally)

A cube has six sides, merely 3 of them can exist visible at a time. So, for the sake of simplicity, we volition focus but on the visible sides (for at present). You lot already know how to construct a horizontal foursquare in every possible position.

This will exist our top airplane.

What is left? The remaining two side planes. Vertical edges are known. They are normal lines to the top airplane.

What is not known is the length of a vertical line. The vertical line is parallel to PP, and so it can't exist foreshortened as much. It gets bigger, when information technology advances in space (like whatever other object) due to a convergence of the lines. So, we assume, that it is a piddling bit longer than the major centrality of our pinnacle ellipse because its major axis tin't be foreshortened every bit well.

In that location is a trick to check if the side planes are right.

Can you guess what it is?

Yes, information technology's ellipse.

Let's put an ellipse with a minor axis pointing at RVP. Ellipse should bear upon midpoints of the plane's edges. Attempt to ghost that ellipse betwixt lines, visualize it. Then we but shut the bottom edge of the left side with a line going to LVP. Finally, nosotros close the right side with a line going to RVP.

The box is done.

Compress Acceleration

Now we have our cube. But you may wonder: how to rotate it in space, how to tilt it? This is a expert question. I like when you ask interesting questions! 😀

To resolve this problem, nosotros must know aboutShrink Dispatch. According to this principle, the shrink of the plane is not linear. In other words, information technology progresses faster and faster as it goes.

We put a cube on the footing plane in a position where the both side planes are at 45 degrees to PP.

At present we plough a cube clockwise. It is still continuing on the ground.

You can see that the left side shrinks more than, then the right side fattens in both accented and relative values.

The more than the plane (or a line) is shrunk, the faster it shrinks.

Even a slight turn of a completely shrunk line makes a dramatic change in its length. As information technology opens more than and more, the speed of opening decreases.

Normal lines do the same thing. When they are parallel to PP, information technology's hard to shrink them. As they plough away from the viewer, it becomes easier and easier to do it.

How to Draw a Cube from Whatsoever Angle in 5 Steps?

The time has come.

Accept my apologies for such a long foreplay. All that stuff is crucial not only for our box cartoon. You will capeesh this material when y'all get onto more than complicated subjects in my later articles.

So, let's exercise it!

• Driblet an ellipse. It can stand for any side of a cube. Your only trouble here is the shrink and direction of a normal.
• Drib normal line according to the desirable front edge position of a cube. Horizon line for this cube volition be actually not horizontal (ha-ha). Information technology simply needs to be perpendicular to the normal of our plane. This is the but requirement.
• Decide on perspective extremeness. Here horizon is out of frame, and the perspective is quite flat.

• Measure out the correct length of a "vertical" corner using an ellipse or just eyeball it. Draw a line to RVP to close the lesser border.
• The terminal side will fall into identify past itself. Just construct correct parallel lines to the ones that already exist.

Homework Assigment

At present it'south time to solidify your knowledge.

Practice it even if you recollect that you already understand how to describe a cube from any angle.

Practice makes perfect, huh? But there should always exist a good noesis base of operations.

I recommend to read this lesson again after the homework is washed.

Hither I've made a demo for yous.
You can see that cubes can overlap each other.

Experience free to play with different sizes and angles. Effort various perspective extremeness. Large boxes can have dramatic convergence of lines.

See yous adjacent time.

libertyandeep.blogspot.com

Source: https://how-to-sketch.com/how-to-draw-a-cube-from-different-angles/

Share this post